Das Digitaloszilloskop und eine verbesserte vertikale Auflösung

Mittelwerte als grundlegende Methode der Signalverarbeitung

Der Mittelwertmodus ist eine der grundlegenden Signalverarbeitungsmethoden zur Rauschunterdrückung im Erfassungssystem des Oszilloskops. Für diesen Modus sind mehrere getriggerte Erfassungen eines wiederholten Signals erforderlich. Der Modus verwendet die Daten aus N = 2, 3, 4, … n und mittelt die entsprechenden Datenpunkte dieser Erfassungen auf Punkt-zu-Punkt-Basis, um das Ausgangssignal darzustellen. Der Mittelwertmodus verbessert das Signal-Rausch-Verhältnis, eliminiert Rauschen, das nicht mit dem Trigger korreliert ist, erhöht die vertikale Auflösung und macht die Anzeige von wiederholten Signalen einfacher.

Bei der herkömmlichen Methode zur Berechnung eines Mittelwertsignals werden einfach die entsprechenden Abtastwerte aus allen Erfassungen summiert und durch die Anzahl der Erfassungen dividiert. Bei dieser Methode wird jedoch der Mittelwert erst angezeigt, nachdem alle gewünschten N Signale erfasst wurden. Eine solche Verzögerung wäre für die meisten Benutzer nicht akzeptabel, außerdem würde das Volumen der Erfassungsdaten die Speicherkapazität des Oszilloskops schnell erschöpfen. A_N = (1 / N) * (x₀ + x₁ + x₂ + … + x_xn-1). Dabei gilt: A_N ist ein Punkt in der gemittelten Erfassung, N gibt die Gesamtzahl der angeforderten Mittelwerte an, x_xn ist ein Punkt in der Erfassung n und n gibt die Erfassungszahl an.

Der herkömmliche Mittelwertalgorithmus kann so modifiziert werden, dass bei jeder neuen Erfassung neue Mittelwerte angezeigt werden. Dadurch wird die Verzögerung kompensiert, die zum Anzeigen des vollständig gemittelten Signals benötigt wird. Das Speicherproblem im Hinblick auf das Datenvolumen bleibt jedoch bestehen. Der Algorithmus für feste Mittelwertbildung lautet: A_N = (1 / N) * (x₀ + x₁ + x₂ + … + x_xn-1). Dabei gilt: A_N ist ein Punkt in der aktuell gemittelten Erfassung, x_xn-1 ist ein Punkt in der neuen Erfassung n und N gibt die Erfassungszahl an. Tektronix-Oszilloskope verwenden einen Algorithmus mit exponentiellem Mittelwert, der die Aktualisierung der Zwischenergebnisse auf dem Bildschirm bei jeder Erfassung erlaubt und den Speicherbedarf erheblich reduziert. Bei der exponentiellen Mittelwertbildung wird folgende Gleichung verwendet, um ein neu gemitteltes Signal a_n aus einer neuen Erfassung x_n und dem bisherigen Mittelwertsignal a_n-1 zu erstellen: a_n = a_n-1 + (1/p)*(x_n – a_n--1 = a_n--1 * ((p – 1) / p) + (x_n / p).

Das resultierende gemittelte Signal ist gleich, unabhängig davon, welcher dieser Mittelwertbildungsalgorithmen verwendet wird. Beachten Sie jedoch, um wie viel effizienter der Algorithmus mit exponentiellem Mittelwert bei der Berechnung und Speicherung der erfassten und gemittelten Signale ist. Einige Oszilloskope kombinieren die beiden vorherigen Methoden, um den Mittelwert zu berechnen. Die erste Erfassung wird angezeigt, für die nächsten N-1 Erfassungen wird feste Mittelwertbildung angewendet, und nach N Erfassungen wird exponentielle Mittelwertbildung angewendet.

Beide Algorithmen zeigen auch die Auswirkungen konsistenter Trends im Signal an. Sie können dies bei einem langsamen Signal leicht erkennen. Wenn das Signal stabil ist, erkennen Sie eine sukzessive Rauschunterdrückung während der ersten N Erfassungen. Nach N Erfassungen ändert sich das Signal zwar noch immer, jedoch verbessert sich die Rauschunterdrückung oder die vertikale Auflösung nicht mehr.

Die Mittelwertbildung erhöht die vertikale Auflösung des Signals. Diese Verbesserung wird in Bit gemessen und ist eine Funktion der Gesamtzahl der Mittelwerte: Verbesserte Auflösung = 0,5 log₂(N), dabei gibt N die Gesamtzahl der angeforderten Mittelwerte an. Bei den Werten in Tabelle 1 handelt es sich um Idealwerte. In vielen Tektronix-Oszilloskopen ist der Mittelwertbildungsalgorithmus mit Fixpunktberechnung implementiert. Die maximale Anzahl der Mittelwerte ist 10.000, wodurch die Gesamtzahl der Bits für die Auflösung auf einen idealen Maximalwert von 14,64 begrenzt wird.

In der Praxis hat die maximale Auflösung durch Fehler der Fixpunktberechnung, durch Rauschen und Jitter-Fehler einen etwas niedrigeren Wert. Idealerweise wird bei der Signal-Mittelwertbildung die volle analoge Bandbreite der Signale beibehalten – ein großer Vorteil gegenüber anderen Signalverarbeitungsmethoden. Erfassungen im Abtastmodus sind jedoch nicht jitterfrei. Das bedeutet, dass die Zeitpunkte der Signalabtastungen nicht mit dem Trigger koordiniert sind. Tatsächlich können die relativen Positionen (dies ist die Definition von Jitter) um ein Abtastungsintervall versetzt sein. Wenn der Frequenzwert gleich dem halben Wert der Abtastrate ist, handelt es sich um einen Phasenfehler von 180 Grad. Der Spitzenwert des Mittelwerts eines solchen Signals ist 0,637 der Signalamplitude oder -3,9 dB. Der Amplitudenfehler aufgrund von Jitter kann durch erhebliches Oversampling des Signals minimiert werden.

Die Bedeutung des HiRes-Erfassungsmodus

Der HiRes-Modus ist ein von Tektronix patentierter Erfassungsvorgang, bei dem der Mittelwert aller aufeinanderfolgenden Abtastwerte in jedem Abtastintervall berechnet und angezeigt wird. Wie der Peak Detect Modus bietet auch der HiRes-Modus eine Methode, Kompromisse zwischen Oversampling und zusätzlichen Informationen zum Signal zu machen. Beim HiRes-Modus wird auf die zusätzlichen Informationen zur horizontalen Abtastung verzichtet, um eine höhere vertikalen Auflösung und eine Reduzierung der Bandbreite und des Rauschens zu ermöglichen. Der HiRes-Modus hat gegenüber dem Mittelwert den großen Vorteil, dass er sogar bei Einzelschuss-Erfassungen verwendet werden kann.

Bandbreitenbegrenzung und Erhöhung der vertikalen Auflösung durch HiRes variieren mit der maximalen Abtastrate und der tatsächlichen (ausgewählten) Abtastrate des Geräts. Die tatsächliche Abtastrate wird normalerweise im unteren Teil des Bildschirms angezeigt, während die maximale Abtastrate im Produktdatenblatt angegeben ist. Die Erhöhung der vertikalen Auflösung in Bit beträgt: 0,5 log₂ * (D), wobei D das Dezimierungsverhältnis oder die maximale Abtastrate/tatsächliche Abtastrate ist. Die resultierende -3 dB Bandbreite (falls nicht weiter begrenzt durch die analoge Bandbreite des Messsystems) beträgt: 0,44 * SR, wobei SR ist die tatsächliche Abtastrate ist.

Das DAC-Ausgabesignal überprüfen

Die erste Anwendung ist das Beurteilen der Signalqualität am Ausgang eines Digital-Analog-Wandlers Das niederfrequente Sinussignal zeigt unkorreliertes Rauschen mit erheblich höherer Frequenz sowie eine Art Stufensignal auf. Auf einer Live-Anzeige ist es deutlicher zu erkennen, dass die Frequenz des Stufensignals nicht mit der Frequenz des Sinussignals übereinstimmt. Da sich am Ausgang des DAC kein Tiefpass-Rekonstruktionsfilter befindet, ist zu erwarten, dass das Signal diskrete Spannungsstufen aufweist. Diese Stufen werden jedoch durch das Rauschen auf dem Signal überdeckt.

Die Mittelwertbildung aus 64 Signalen ist ein sehr zeitaufwändiger Vorgang mit sehr langen Aufzeichnungen. Wie erwartet, wird das unkorrelierte Rauschen erheblich gedämpft, und die diskreten Spannungsstufen des DAC werden langsam sichtbar. Da die Abtastrate extrem hoch ist, bleibt außerdem die volle Messbandbreite erhalten. Da das Stufensignal jedoch nicht mit dem Triggersignal korreliert ist, wird durch die Mittelwertbildung auch das Stufensignal aus der gemittelten Anzeige entfernt.

Da es sich jedoch um eine Einzelschuss-Verarbeitungsmethode handelt, bleibt das niederfrequente Stufensignal erhalten. Außerdem wurde durch die Anwendung des HiRes-Erfassungsmodus die vertikale Auflösung auf etwa 12 Bit erhöht, und die Messbandbreite wurde auf etwa 22 MHz reduziert.

Das Taktsignalspektrum mit 40 MHz messen

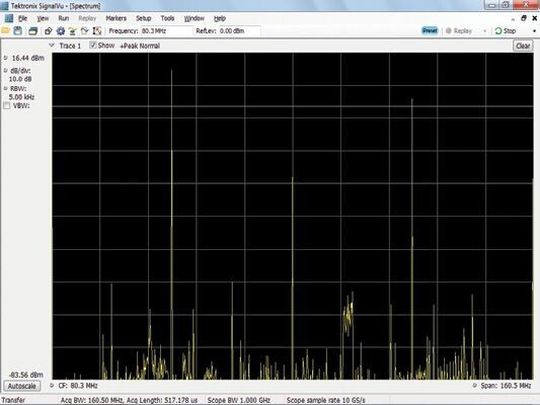
Die zweite Anwendung ist die Spektralanalyse eines digitalen Taktsignals von 40 MHz. Digitale Signale übertragen Informationen in der zeitlichen Position der Signalflanken (gemessen beim Überschreiten einer Schwelle) und zumeist nicht der Signalamplitude. Die Signal-Mittelwertbildung ist sehr effizient beim Entfernen von nichtkorreliertem Rauschen aus kontinuierlichen Signalen wie diesem.

Die Spektralanalyse ermöglicht, zum Teil aufgrund ihrer logarithmischen vertikalen Skala, eine sehr empfindliche Messung der Rauschreduzierung durch die Mittelwertbildung. Beachten Sie, dass die vertikalen Skalen in den Bildern 16 und 17 auf 10 dB/DIV eingestellt sind. Bild 17 zeigt, dass die Größe der grundlegenden und ungeraden Oberschwingungen relativ konstant bleibt, jedoch durch die Mittelwertbildung das Basislinienrauschen um 10 bis 20 dB reduziert wird und auch viele der anderen Komponenten reduziert werden, sodass die Oberschwingungen und anderen Störsignale des Taktsignals leichter zu identifizieren sind.

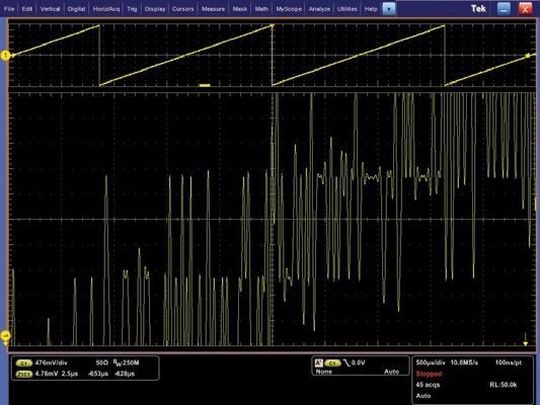
Das dritte Beispiel ist eine Methode zur Veranschaulichung der tatsächlichen Verbesserung der vertikalen Auflösung mit einem hochauflösenden DAC oder, in diesem Fall, einem hochauflösenden Arbiträrsignalgenerator der Serie AWG7000. Bild 18 zeigt eine gezoomte Anzeige eines Rampensignals mit einer vertikalen Auflösung von 10 Bit. Obwohl im unteren Bereich der Anzeige diskrete 8-Bit-Stufen zu erkennen sind, ist das Rauschen auf dem Signal groß genug, um gelegentliche Fehler von ±1 Bit zu verursachen. Bei dieser 8-Bit-Auflösung sind diese Fehler erheblich größer als die 10-Bit-Stufen auf dem Rampensignal.

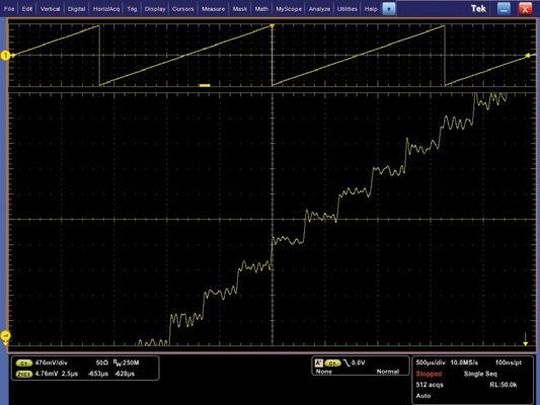
Die Signal-Mittelwertbildung verbessert das die Signal-Mittelwertbildung. In diesem Fall heben sich die einzelnen 10-Bit-Stufen deutlich vom Digitalisierungsrauschen ab. Das demonstriert die Fähigkeit eines 8-Bit-ADC, mithilfe einer Signalverarbeitungsmethode wie der Signal-Mittelwertbildung eine vertikale Auflösung von mindestens 10 Bit zu erreichen.

* Trevor Smith ist bei Tektronix für das technische Marketing in der EMEA-Region verantwortlich.

(ID:32945430)